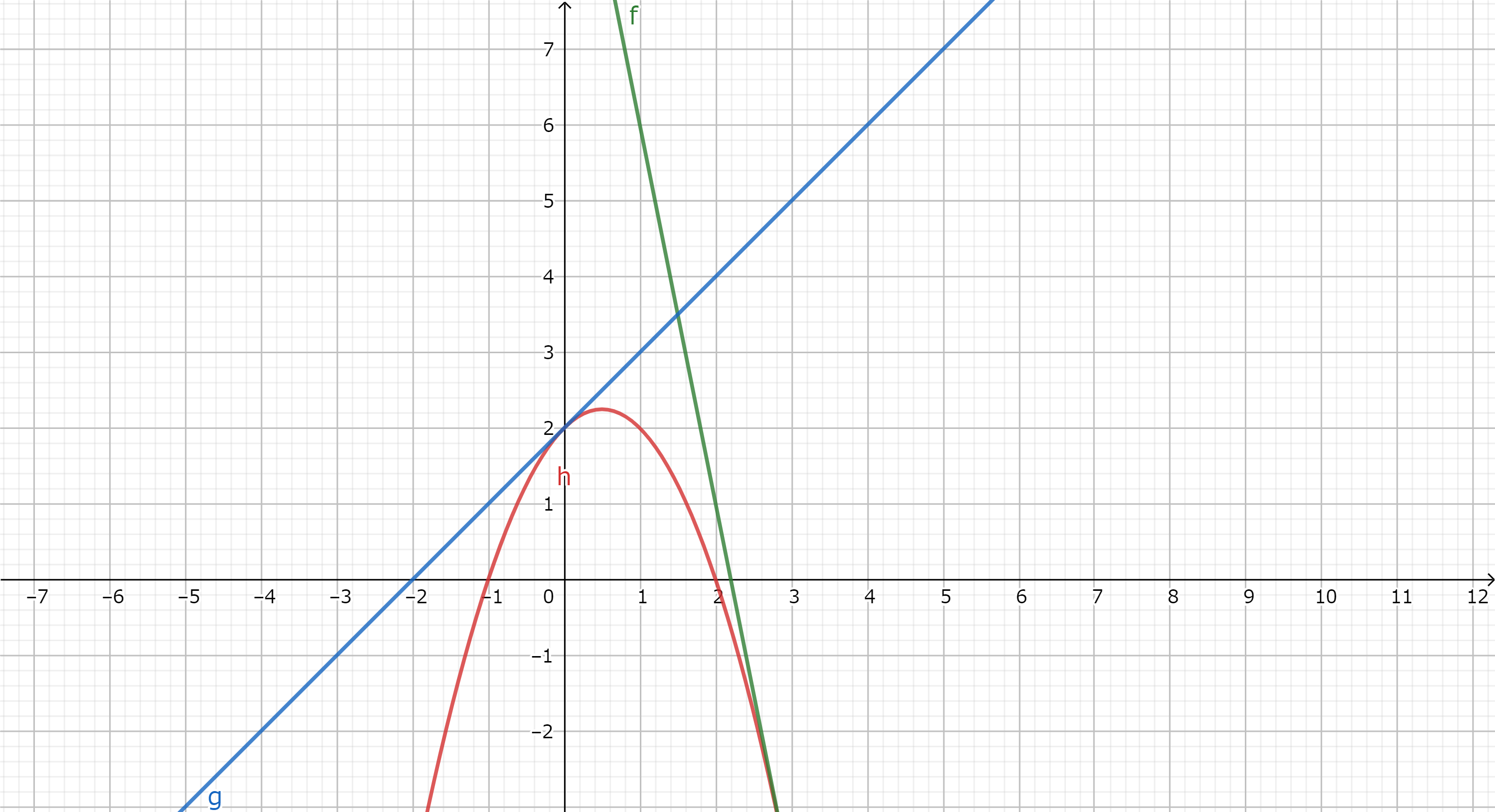
二次関数の最大・最小 201025

x についての二次関数 \(f(x)=x^2-2kx+k+2\)について
k は定数とします。
0 ≦ x ≦ 3 における f(x) の最大値を M, 最小値を m とします。
M, m を k を用いて表してみましょう。

思い切って，一般化してみます。
\(f(x)=(x-k)^2+q\) とします。
q は x については定数であるとします。一般には k については関数となりますが， f(k) = q ですので，
\(f(x)=(x-k)^2+f(k)\) と表すことができます。

いま，x² の係数は 1 で正の数ですから，
f(x) は x ≦ k で単調に減少する
f(x) は k ≦ x で単調に増加するので
x = k で最小値 f(k) をとります。

区間 a ≦ x ≦ b における f(x) のとりうる値の範囲を考えてみましょう。
この区間における f(x) の
最大値を k の関数として，M(k)
最小値を k の関数として，m(k) と書くことにします。
区間の制限を外して，最小値の定義から任意の x に対して f(x) ≧ f(k) が成り立ちます。
特に， f(a) ≧ f(k), f(b) ≧ f(k) です。
f(k) は k の関数ですので，，m₀(k) と書くことにします。
f(a) は k の関数ですので，，m_a(k) と書くことにします。
f(b) は k の関数ですので，，m_b(k) と書くことにします。

最小値 m(k) については，

(i) a ≦ k ≦ b のとき，m(k) = m₀(k) となります。

(ii) k < a のとき，
区間 a ≦ x ≦ b では f(x) は単調に増加しますので，
m(k) = f(a) ( = m_a(k) )

(iii) b < k のとき，
区間 a ≦ x ≦ b では f(x) は単調に減少しますので，
m(k) = f(b) ( = m_b(k) )

最大値 M(k) について考えてみます。
最大値は f(a) か f(b) ですので，
まず，f(a) = f(b) となる k の値を求めてみます。
\(f(b)-f(a)=(b-k)^2-(a-k)^2\) \(=(b-a)(a+b-2k)\)
いま, a は b より小さいので， f(a) = f(b) となるのは \(k=\frac{a+b}{2}\)のときです。
また，
\(k< \frac{a+b}{2}\) のとき f(a) < f(b)
\(k> \frac{a+b}{2}\) のとき f(a) > f(b)
であることがわかります。

(i) \(k=\frac{a+b}{2}\) のとき，M(k) = f(a) = f(b) となります。

(ii) \(k < \frac{a+b}{2}\) のとき， M(k) = f(b) ( = m_b(k) )

(iii) \(k > \frac{a+b}{2}\) のとき， M(k) = f(a) ( = m_a(k) )

M(k), m(k) をグラフにしてみましょう。
M(k), m(k) は m_a(k), m_b(k), m₀(k) の3つの式で表されます。
ここで，f(a), f(b), f(k) の関係から
\(m_a(k)=m_0(k)+(k-a)^2\), \(m_b(k)=m_0(k)+(k-b)^2\) です。
また，\(m_a\left(\frac{a+b}{2}\right)=m_b\left(\frac{a+b}{2}\right)\)

さらに，
\(m_a(k)-m_0(k)=(k-a)^2\) より，
\(\frac{d}{dk}(m_a(k)-m_0(k))=2(k-a)\)
m_a(a) = m₀(a) = m(a)
2つのグラフ y = m_a(k) と y = m₀(k) は点(a, m(a)) で共通の接線をもちます。点(b, m(b)) についても同様です。

再考 二次関数の最大・最小

再考二次関数の最大・最小