三角形の外心 220311

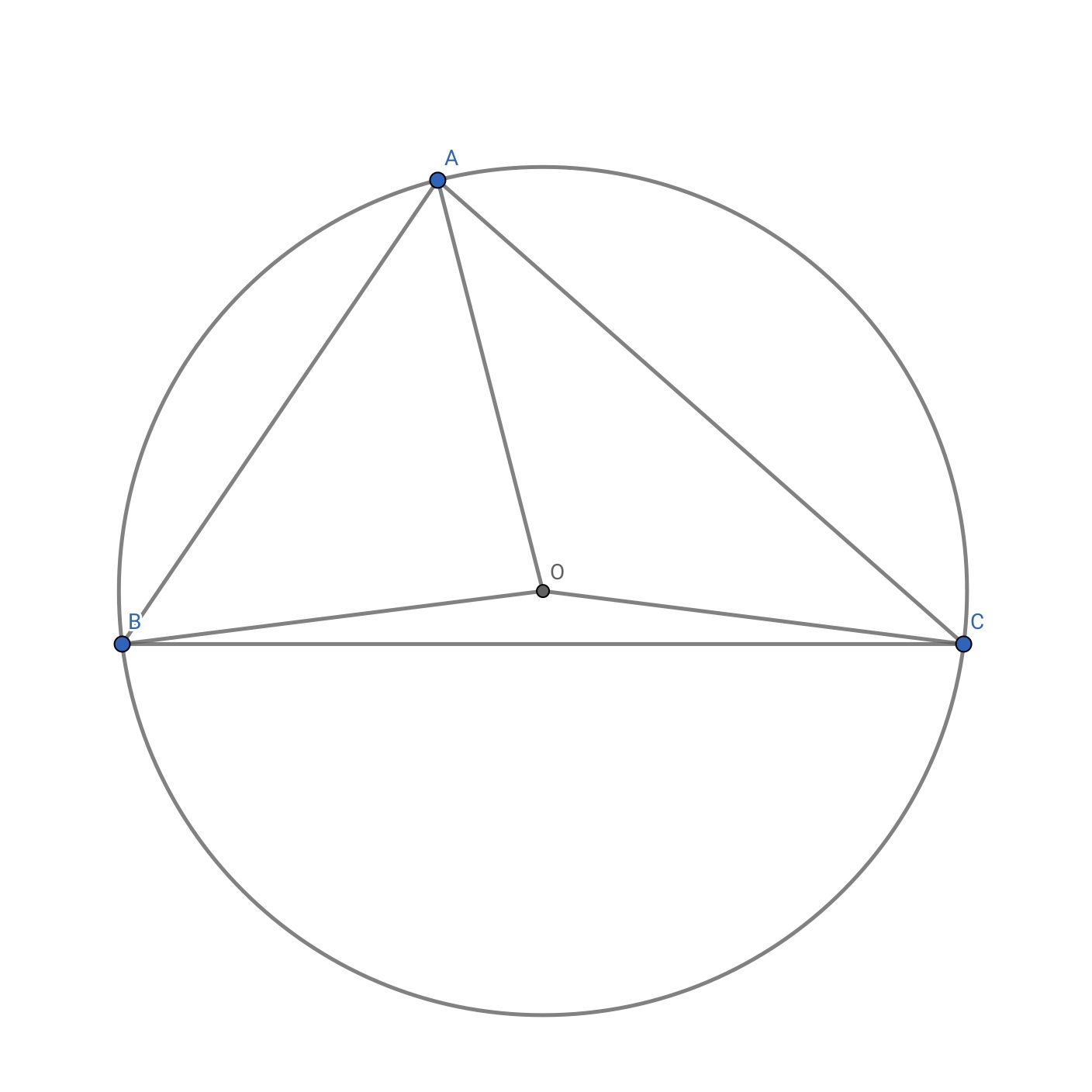
辺AB の垂直二等分線と 辺AC の垂直二等分線の交点をO とします。
すると、OA = OB かつ OA = OC が成り立ちます。
よって、OA = OB = OC だから、 O は辺BC の垂直二等分線上にあります。
つまり、3本の辺の垂直二等分線は1点で交わります。
O は3点A, B, C から等距離にあるので、 A, B, C で決まる円の中心です。
この円を三角形ABC の外接円、 点O を三角形ABC の外心といいます。

三角形の3辺の長さが与えられているとします。
外接円の半径 R を求めてみましょう。
余弦定理によって、cos A がわかります。
sin² A + cos² A = 1 が成り立ちますから、sin A がわかります。
よって、正弦定理によって R がわかります。

O の位置はどのように求めればよいでしょうか。
A, B, C の位置が与えられたとすると、 垂直二等分線の交点で決定することができます。
外接円の方程式から中心を求めることもできます。

外心の取り扱いはベクトルが便利です。
\(\overrightarrow{\rm AB}=\vec{b}\), \(\overrightarrow{\rm AC}=\vec{c}\) とおきます。
\(\vec{b}\), \(\vec{c}\), \(\vec{b}\cdot\vec{c}\) が与えられたとします。
\(\overrightarrow{\rm AO}=x\vec{b}+y\vec{c}\) と表したとき、 x, y を求めてみましょう。

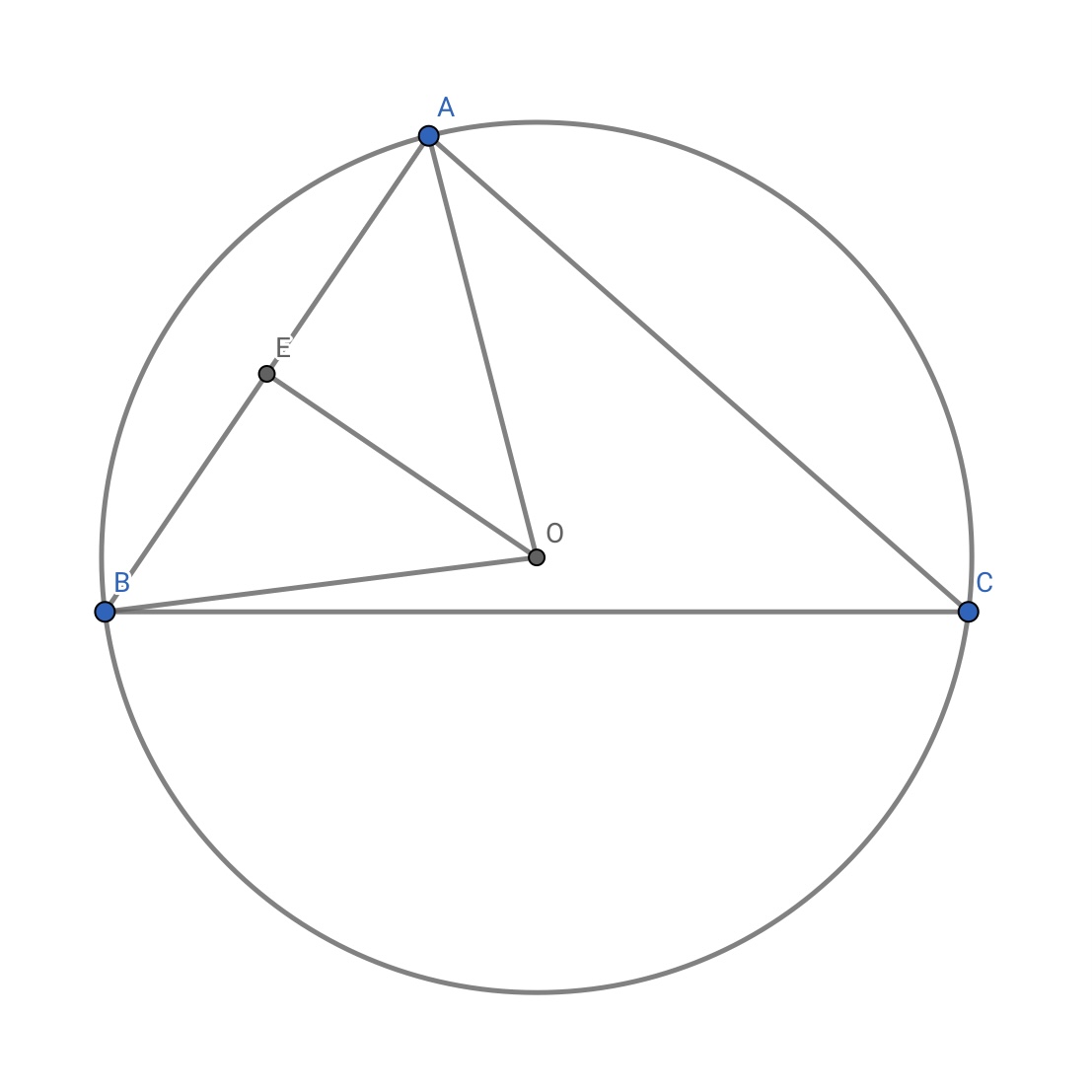
\(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AO}\) を考えます。
内積の定義より、
\(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AO}\) \(={\rm AB}\cdot{\rm AO}\cdot\cos\angle{\rm BAO}\)
三角形OAB は二等辺三角形だから、 AB の中点を E とすると、三角形OAE は直角三角形です。
すると、 \({\rm AO}\cdot\cos\angle{\rm BAO}={\rm AE}\)
ゆえに、 \(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AO}\) \(=\dfrac{1}{2}{\rm AB}^2\)
同様に、 \(\overrightarrow{\rm AC}\cdot\overrightarrow{\rm AO}\) \(=\dfrac{1}{2}{\rm AC}^2\)
一方、
\(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AO}\) \(=x\vec{b}\cdot\vec{b}+y\vec{b}\cdot\vec{c}\)
\(\overrightarrow{\rm AC}\cdot\overrightarrow{\rm AO}\) \(=x\vec{b}\cdot\vec{c}+y\vec{c}\cdot\vec{c}\)
したがって、x, y を求めることができます。