二次関数 増減 最大・最小 (1) 220203

関数\(f(x)\) と ある区間で，
その区間の任意の2数\(x_1\), \(x_2\)に対して，
\(x_1< x_2\) ならば \(f(x_1)< f(x_2)\) が成り立つとき
\(f(x)\)はこの区間で単調に増加している といいます。

みんなでGeoGebra YouTube 増減 最大・最小
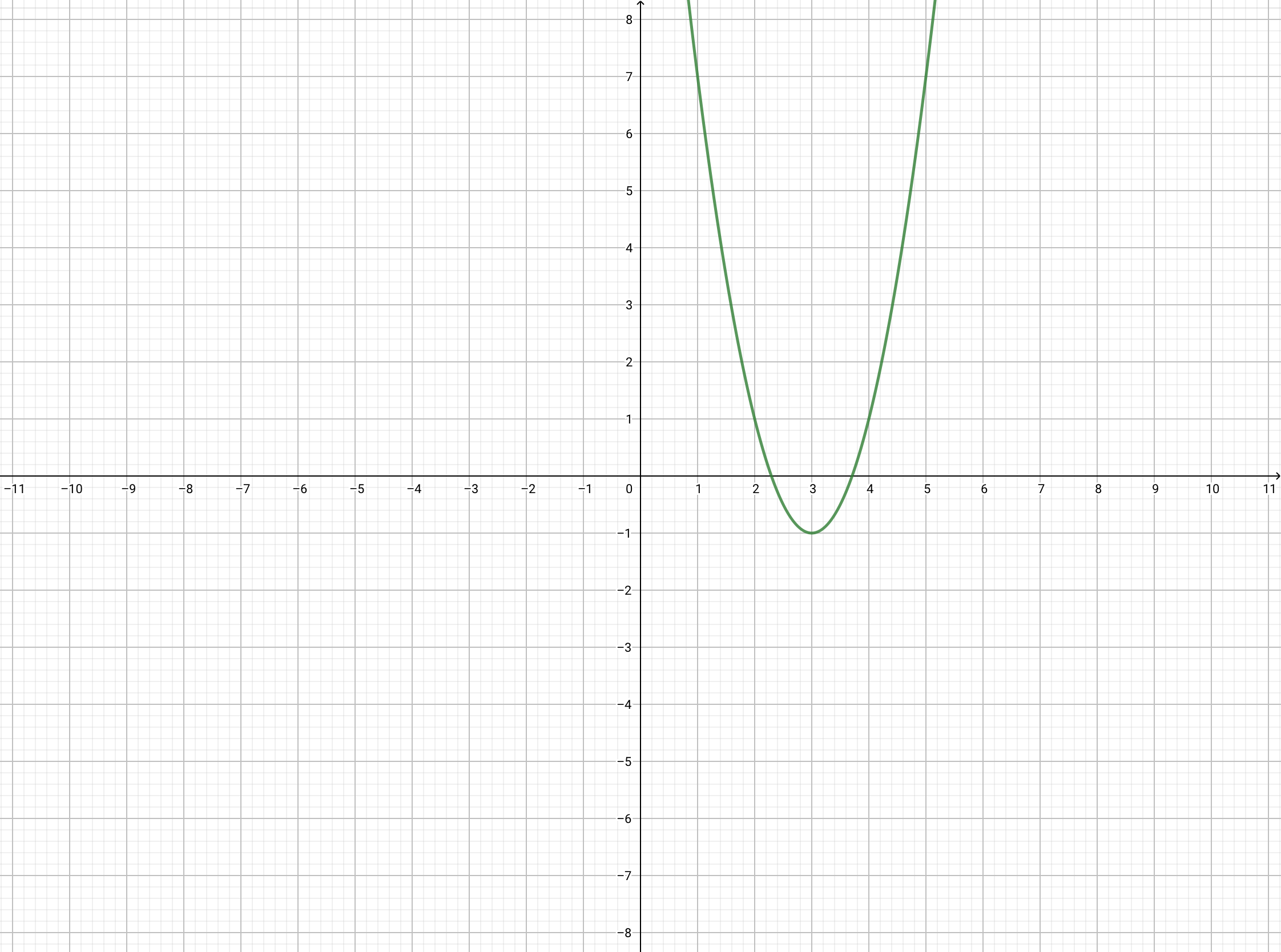
\(f(x)=2(x-3)^2-1\)…① として，\(y=f(x)\) のグラフをかいてみよう。
\(f(x)\) は 区間 \(x\geqq 3\) において， 単調に増加しているようです。
実際，\(3\leqq x_1< x_2\) なる2数に対して，
\(f(x_2)-f(x_1)\) を計算すると，\(2(x_2-3+x_1-3)(x_2-x_1)\) となることから
\(f(x_2)> f(x_1)\) が分かります。
\(x_1\) は 3 でもよいので，
\(x\geqq 3\) において単調に増加している といってよいのです。
また， \(x\leqq 3\) において単調に減少しています。

\(x\) として，ある区間(変域，定義域)の値をとるとき， \(f(x)\) のとりうる値の集合(範囲)(値域)を考えます。
このとりうる値の集合に最も大きい値があれば，それを最大値といいます。
関数① は，\(x=3\) で最小値\(-1\) をとります。最大値はありません。

いろいろな\(a\), \(p\), \(q\) の値で，
\(a(x-p)^2+q\) の増減が式を見ただけでわかるようになるといいですね。 式とグラフとの結びつきもわかるようになるといいですね。
あとは， 2次式\(ax^2+bx+c\) が \(a(x-p)^2+q\) の形に 変形できる(平方完成)ようになると， 2次関数の値の変化の様子や放物線がかなり分かってきます。