三角関数の加法定理

三角関数の性質B で見たように，
\(\sin\left(\alpha+\dfrac{\pi}{2}\right)=\cos\alpha\),   \(\cos\left(\alpha+\dfrac{\pi}{2}\right)=-\sin\alpha\)
が成り立ちます。

OP を斜辺とする 直角三角形OAPで，
OP = 1, 角POA の大きさを α とします。
O を中心に反時計回りに β だけ三角形を回転させます。
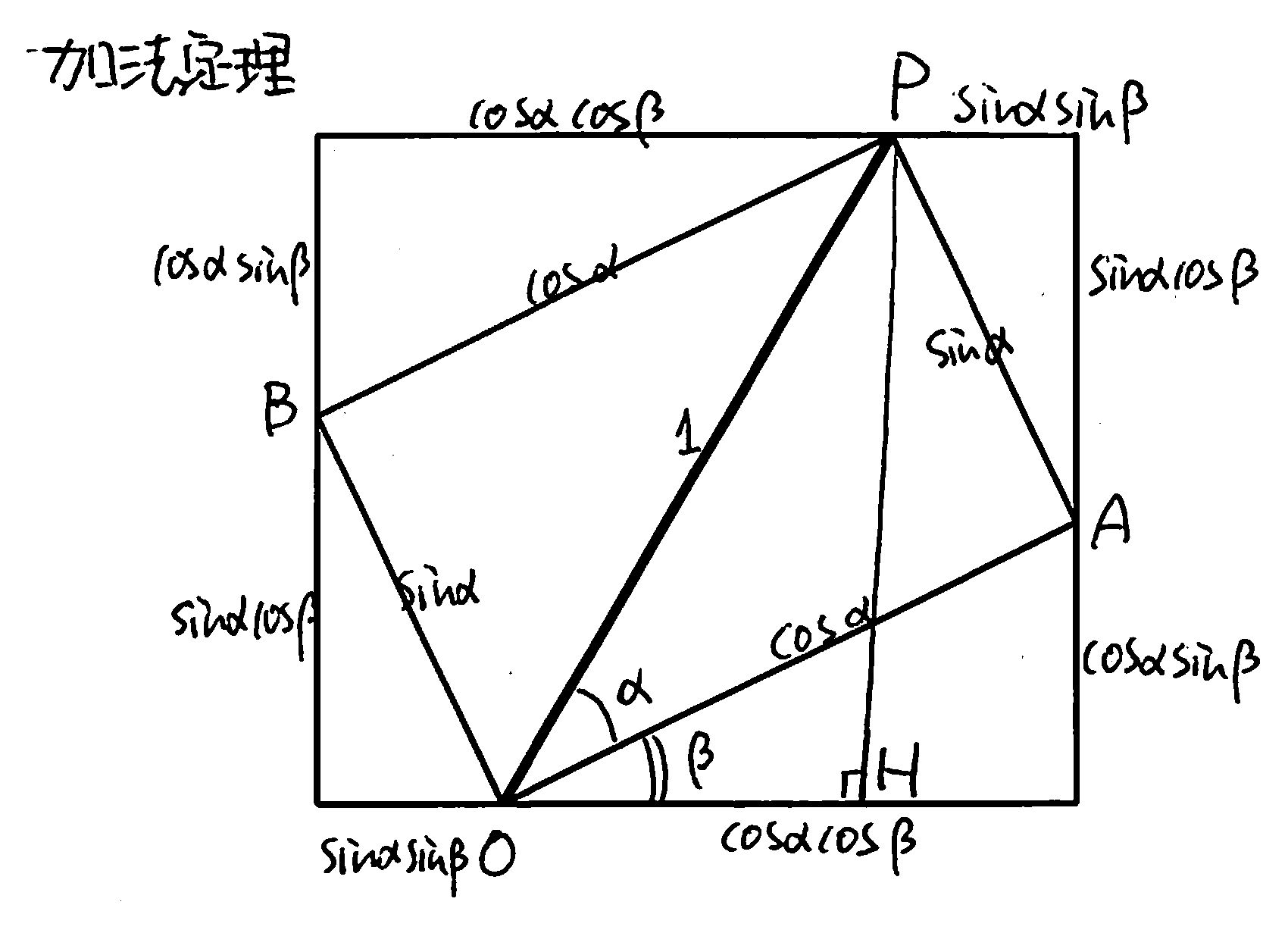
加法定理 説明図 (svg)

∠POA = α,  ∠AOJ = β です。
三角比の定義により，
OA = cos α,  AP = sin β
OH = cos (α + β),  PH = sin (α + β)
さらに，三角比の定義により
AJ = cos α sin β,  AK = sin α cos β
OJ = cos α cos β,  PK = sin α sin β

したがって，
sin (α + β) = sin α cos β + cos α sin β
cos (α + β) = cos α cos β - sin α sin β
この式は，α, β がどんな大きさの角でも成り立ちます。
三角関数の加法定理といいます。

ちなみに，
\(\beta=\dfrac{\pi}{2}\) とすると， 冒頭の式が出てきますし， 工夫すると性質Bが出てきます。

　正接については，相互関係より
\(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)